Pour un développement de la compétence en résolution de problèmes

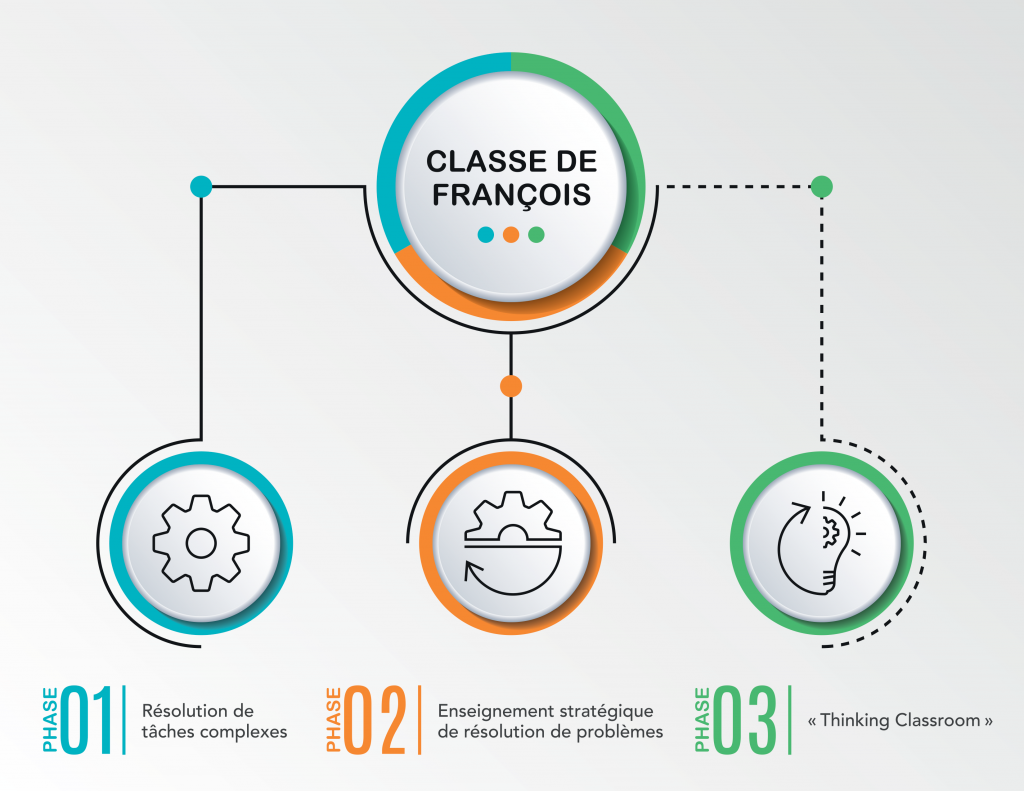
Pour un développement de la compétence en résolution de problèmes

La seule accumulation de connaissances n’est pas suffisante pour développer la capacité des élèves à résoudre des problèmes ou des tâches complexes faisant appel à plusieurs concepts différents et nécessitant plusieurs étapes pour arriver à une solution.

Avec les nouvelles évaluations, il devient primordial de travailler cet aspect avec les élèves en plus de leur apprendre les différents savoirs du programme. C’est pourquoi je prévois des périodes pour travailler la résolution de problèmes avec mes élèves et d’autres périodes pour leur enseigner explicitement l’utilisation de quelques stratégies de résolution de problèmes qui permettent de résoudre un grand nombre de problèmes.

La résolution de problèmes en équipe

Autant que possible, chaque élève dans ma classe résout un problème par semaine en équipe de 2 ou 3. Les tâches complexes proposées sont toujours en lien avec le cours actuel de l’élève afin qu’il puisse avoir l’occasion de résoudre plusieurs tâches complexes en lien avec son cours pendant qu’il suit celui-ci. 

Les notions préalables à la résolution du problème ont généralement été vues avant la résolution du problème, mais pas toujours. Un problème peut aussi être une bonne occasion pour enseigner de la nouvelle matière. La résolution de problèmes pourrait être faite seule, mais je privilégie les équipes de deux ou trois, car la verbalisation et la confrontation des idées sont importantes pour le développement des compétences, d’où l’importance du travail d’équipe (réf. Socioconstructivisme, Vygotski, 1997). Le fait de placer les élèves en équipe permet aussi, bien  souvent, d’économiser du temps, car on peut expliquer la même chose à plus d’un élève à la fois et les élèves peuvent également s’aider à comprendre des notions et des éléments du problème qu’ils doivent résoudre.

Pour l’enseignant, il est important de questionner ses élèves tout au long de la démarche pour les guider dans la résolution et les aider à développer leur comportement stratégique. L’utilisation de stratégies implique de faire des choix. Faire des choix, c’est tout d’abord de se poser des questions. Si l’on réussit à amener l’élève à avoir le réflexe de se questionner, il utilisera davantage de stratégies et sera plus apte à résoudre des problèmes. Cette méthode tient également compte du fait que les élèves ne choisissent pas tous la même stratégie pour arriver à résoudre un même problème mathématique. Souvent, ils peuvent résoudre un problème en utilisant de multiples combinaisons de stratégies (Ornstein et Lasley, 2004).

L’enseignement explicite de stratégies de résolution de problèmes

Le questionnement et la résolution de problèmes à eux seuls ne sont pas toujours suffisants pour que l’élève utilise les bonnes stratégies de résolution. Il doit également connaitre et maitriser une stratégie pour l’utiliser. C’est pourquoi il est bénéfique d’enseigner certaines stratégies de résolution, notamment des stratégies de visualisation du problème, par exemple se faire un dessin, et des stratégies de planification des étapes de résolution, par exemple se faire un plan de résolution du problème en réfléchissant à rebours. 

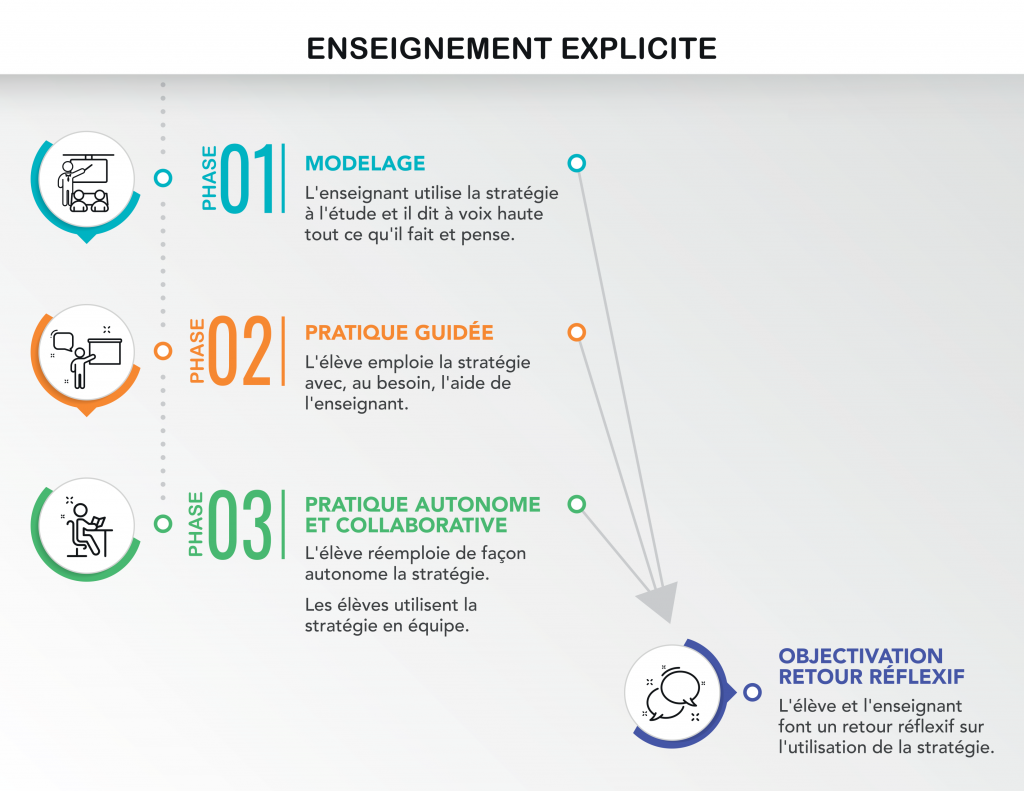
L’enseignement explicite permet d’enseigner des stratégies importantes de résolution de problèmes. Cet enseignement peut être fait en grand groupe (comme dans la vidéo), en sous-groupes ou individuellement.

Dans un premier temps, l’enseignant fait un modelage de la stratégie, en montrant aux élèves comment il applique la stratégie.

Modelage par l’enseignant

Dans un deuxième temps, l’élève (un élève du groupe lorsque l’enseignement se fait en groupe) fait une pratique guidée; il applique la stratégie que l’enseignant vient de modéliser. L’enseignant accompagne l’élève en lui posant des questions lorsqu’il est coincé, mais il lui laisse tout de même le temps de réfléchir auparavant.

Pratique collaborative entre élèves

Finalement, l’élève utilise la stratégie de manière autonome. Personnellement, j’ajoute une partie de pratique collaborative, où les élèves appliquent la stratégie enseignée en équipe de deux ou trois élèves. Je circule en classe durant cette période afin d’aider les équipes dans leur démarche.

En résumé, une période où j’enseigne explicitement une stratégie de résolution de problèmes se fait en 3 temps :

• 1re étape – Modelage : Je montre comment moi j’applique la stratégie
• 2e étape – Pratique guidée : Un élève applique la stratégie modelée devant les autres élèves avec mon aide
• 3e étape – Pratique collaborative : Les élèves appliquent la stratégie modelée en équipe de deux ou trois et je circule dans la classe pour valider que tous les élèves aient bien compris. Chacune de ces étapes est suivie d’un retour réflexif pendant lequel je fais un retour avec les élèves sur les grandes étapes de l’application de la stratégie. L’extrait suivant est le retour réflexif suivant la pratique guidée vue plus haut.

 

Évolution et difficultés rencontrées

2012 : Début du travail de résolution de problèmes en équipes dans un groupe de FBC, tout le groupe, une fois par semaine

2017 : Implantation de la résolution de tâches complexes en FBD

2019 : Début de l’enseignement explicite de stratégies en grand groupe

Au début du projet, quelques élèves étaient réticents et résistaient au travail d’équipe. La culture du cahier était encore bien ancrée en eux et ils avaient l’impression d’être ralentis par les périodes de travail en équipe. Ces résistances se sont atténuées à force de persévérance de ma part et lorsque des résultats positifs ont été perçus par certains élèves. 

L’implantation de cette méthode de travail a été un peu plus ardue en FBD. En FBC, les groupes étant plus restreints et le nombre de sigles moindre, il est possible de faire travailler tout le groupe en même temps sur des tâches complexes. En FBD, avec 25-30 élèves et la multitude de sigles de cours, l’expérience n’a pas été concluante du tout. Je me suis retrouvé rapidement débordé et les élèves décrochaient, car ils n’avaient pas l’accompagnement nécessaire. Il m’a fallu me réajuster en ne faisant travailler que quelques équipes à la fois en résolution de tâches complexes  et garder les autres dans leur cahier.https://www.high-endrolex.com/34

L’enseignement explicite de stratégies de résolution de problèmes pose lui aussi son lot de défis. Bien que toutes les stratégies soient utiles à connaitre pour les élèves, certaines sont plus pertinentes dans certains cours, d’autres moins. L’enseignement en grand groupe est efficace, car tous les élèves ont la chance de voir la stratégie, mais certains d’entre eux ne pourront la réinvestir que beaucoup plus tard. C’est pourquoi il pourrait être préférable de faire des sous-groupes. Si c’est l’option choisie, il importe toutefois de bien planifier la séquence, car il ne faut pas que les élèves qui ne sont pas concernés soient laissés à eux-mêmes trop longtemps.

Impacts sur l’apprentissage

Les élèves sont mieux outillés pour faire leurs examens et semblent mieux préparés. Ils savent plus à quoi s’attendre et se sentent moins démunis. La résolution de problèmes reste difficile, mais les élèves savent qu’ils sont capables et ont moins tendance à abandonner pendant l’examen. Une élève parle ici des impacts de cette méthode sur elle.

Conclusion

Bien qu’elle me demande un peu plus de travail, l’ajout de ces deux activités à mon enseignement traditionnel dans le cahier a contribué à dynamiser ma classe et à développer la capacité de mes élèves à résoudre des problèmes et ainsi à mieux réussir les examens du renouveau. 

Je n’ai pas encore trouvé la formule parfaite ou idéale, mais plus le temps avance et plus je m’approche d’une pratique enseignante qui favorise réellement le développement de compétences. Récemment, on m’a partagé un article sur le « thinking classroom » (La classe qui pense, traduction libre, voir la section « plus d’information » pour la publication originale en anglais). 

Je travaille donc présentement à ajuster les périodes de travail sur la résolution de problèmes de manière à favoriser encore plus l’apprentissage de la résolution de problèmes chez mes élèves. Les résultats préliminaires semblent prometteurs et pourraient faire l’objet d’une prochaine céramique… À suivre! 

Plus d’informations

• Séquences d’enseignement explicite de stratégies (sous l’onglet « Ateliers Résolution de problèmes »): https://16.ticfga.ca/2019/09/18/strategies-de-lecture-et-de-resolution-de-problemes/
• Banque de tâches complexes :  https://drive.google.com/drive/folders/1lUTs8XQcZyHT1QmO3Zazj9rQRMBC-mif?usp=sharing
• Building a Thinking Classroom in Math (en anglais): https://www.edutopia.org/article/building-thinking-classroom-math

 

Ressources créées par :

• François P. Lagacé, enseignant de mathématique 
• Sonia Boulais, infographiste CSSMI

Remerciements particuliers :

• Vanessa Boily, conseillère pédagogique Équipe-choc pédagogique
• Marie-Ève Ste-Croix, conseillère pédagogique RÉCIT FGA (courriel, twitter, site Web)

Si vous souhaitez plus d’informations sur ces ressources ou si vous souhaitez ajouter quelque chose à cette céramique, veuillez contacter l’un des conseillers mentionnés ci-dessus. Toutes les ressources doivent être réutilisées et partagées conformément à la licence Creative Commons suivante : CC BY-NC-SA 4.0